关于PCA算法的一点思考

12 Jul 2020 Machine-Learning

PCA是机器学习中一种常用的降维方法，从优化的角度上来说，PCA的意义很丰富，但是并不难理解，其中主要让我困惑的一点是为什么PCA这种贪心算法找到的结果是全局最优？

通常介绍PCA的文章会提供两个理解的角度：

• 最大化投影方向的方差
• 最小化平方误差

以下首先给出这两种理解的证明，然后给出为什么PCA得到的结果是全局最优。

$$\def\bm#1{\boldsymbol{#1}}$$

最大化投影方向的方差

设有一组去中心化后的$p$维数据向量$(x_1, x_2, \cdots, x_n)$，写成矩阵形式$\bm{X} \in \mathcal{R}^{n\times p}$，PCA的想法是首先寻找一个投影方向$\omega$，使得数据在这个方向上的投影的方差最大，即

$$\left\{\begin{aligned} & \hat{\omega} = \underset{\omega}{\mathrm{argmax}} \sum\limits_{i=1}^n (\omega^T x_i)^2 \\ & \text{s.t. } \omega^T\omega = 1\end{aligned} \right.$$

以上优化问题可以转化为

$$\begin{aligned} \hat{\omega} & = \underset{\omega}{\mathrm{argmax}} \left[\sum\limits_{i=1}^n (\omega^T x_i)^2 \right] \\ & = \underset{\omega}{\mathrm{argmax}} \left[ \sum\limits_{i=1}^n \omega^T x_ix_i^T \omega \right]\\ & = \underset{\omega}{\mathrm{argmax}} \left[ \omega^T (\sum\limits_{i=1}^n x_i x_i^T) \omega \right] \\ & = \underset{\omega}{\mathrm{argmax}}\left[ \omega^T \bm{X}^T \bm{X} \omega\right] \end{aligned}$$

注意到$\bm{X}^T\bm{X}$/(n-1) 即样本的协相关矩阵（数据已去中心化）。为了求解包含约束的优化问题，引入含拉格朗日乘子的函数

$$F(\omega) = \omega^T \bm{X}^T\bm{X}\omega - \lambda \omega^T \omega + \lambda$$

对$\omega$求导得到，

$$\frac{\partial F}{\partial \omega} = 2 \bm{X}^T\bm{X}\omega -2\lambda\omega$$

导数为零时取得极值，即

$$\bm{X}^T\bm{X} \hat{\omega} = \lambda\hat{\omega}$$

二阶导数为$\frac{\partial^2 F}{\partial \omega\partial \omega} = 2\bm{X}^T\bm{X} - 2\lambda \bm{I}$（因为$\lambda$为$\bm{X}^T\bm{X}$的最大特征值，$\bm{X}^T\bm{X}-\lambda\bm{I}$的特征值非正，因此$\bm{X}^T\bm{X}-\lambda\bm{I}$为半负定矩阵。）

因此，$F(\omega)$取得极值的方向即$\bm{X}^T\bm{X}$的特征方向，此时$F(\omega) = \lambda$为特征值，所以$\hat{\omega}$即为$\bm{X}^T\bm{X}$的最大特征值对应的特征向量。

将上一步得到的$\hat{\omega}$设为$\hat{\omega_1}$，接下来，寻找一个新的投影方向$\omega_2$，要求数据在这个方向上投影的方差最大，同时$\omega_2$与$\omega$正交，即

$$\left\{ \begin{array}{l} \hat{\omega}_2 = \underset{\omega_2}{\mathrm{argmax}} \sum\limits_{i=1}^n (\omega_2^T x_i)^2 \\ \text{s.t. } \omega_2^T\omega_2 = 1 \text{ and } \omega_2^T \omega_1 =0 \end{array} \right.$$

类似地，采用拉格朗日乘子法，得到

$$F(\omega_2) = \omega_2^T \bm{X}^T\bm{X}\omega_2 - \lambda \omega_2^T \omega_2 + \lambda + \phi\omega_2^T \omega_1$$

对$\omega_2$求偏导，

$$\frac{\partial F}{\partial \omega_2} = 2 \bm{X}^T\bm{X}\omega_2 -2\lambda\omega_2 + \phi\omega_1=0$$

两端乘以$\omega_1^T$，得到

$$\phi = -2\omega_1^T\bm{X}^T\bm{X}\omega_2 = -2 \omega_2^T\bm{X}^T\bm{X}\omega_1=-2\lambda_1\omega_2^T\omega_1 = 0$$

此时，同样地

$$\bm{X}^T\bm{X}\omega_2 = \lambda\omega_2$$

即$\omega_2$为$\bm{X}^T\bm{X}$的第二大特征值对应的特征方向。

以此类推，得到$\omega_3,\cdots, \omega_d$。

最小化平方误差

设有一组去中心化后的$p$维数据向量$(x_1, x_2, \cdots, x_n)$，写成矩阵形式$\bm{X} \in \mathcal{R}^{n\times p}$。我们希望找到一组正交基向量（$\omega_1, \cdots, \omega_d$）（对应一个$d$维子空间 $\bm{W} = (\omega_1, \cdots, \omega_d) \in \mathcal{R}^{p \times d}$），使得数据向量在这个子空间的投影向量$\bm{W}\bm{W}^Tx_i$与原向量的差的平方和最小。投影向量也可以看做是$\bm{X}$在子空间的重构向量，所以优化目标也就是最小化重构误差（reconstruction error）。写成数学形式，即

$$\begin{aligned} W & = \underset{W}{\mathrm{argmin}}\left[ \sum\limits_{i=1}^n ||\bm{W}\bm{W}^Tx_i -x_i||^2 \right] \\ & = \underset{W}{\mathrm{argmin}}\left[ \sum\limits_{i=1}^n (\bm{W}\bm{W}^Tx_i -x_i)^T (\bm{W}\bm{W}^Tx_i -x_i) \right] \\ & = \underset{W}{\mathrm{argmin}}\left[ \sum\limits_{i=1}^n (x_i^T \bm{W}\bm{W}^T \bm{W} \bm{W}^T x_i -x_i^T \bm{W}\bm{W}^Tx_i - x_i^T \bm{W}\bm{W}^Tx_i + x_i^T x_i) \right] \\ (\bm{W}^T\bm{W}=\bm{I}_d) & = \underset{W}{\mathrm{argmin}}\left[ \sum\limits_{i=1}^n ( - x_i^T \bm{W}\bm{W}^Tx_i + x_i^T x_i) \right] \\ (x_i^T x_i = \mathrm{const.}) & = \underset{W}{\mathrm{argmin}}\left[ \sum\limits_{i=1}^n ( - x_i^T \bm{W}\bm{W}^Tx_i) \right] \\ & = \underset{W}{\mathrm{argmax}}\left[\sum\limits_{i=1}^n \mathrm{tr}( x_i^T \bm{W}\bm{W}^Tx_i) \right] \\ & = \underset{W}{\mathrm{argmax}}\left[\sum\limits_{i=1}^n \mathrm{tr}( \bm{W}^Tx_i x_i^T \bm{W})\right] \\ & = \underset{W}{\mathrm{argmax}}\left[\mathrm{tr}\left(\sum\limits_{i=1}^n \bm{W}^Tx_i x_i^T \bm{W}\right)\right] \\ & = \underset{W}{\mathrm{argmax}}\left[\mathrm{tr}\left( \bm{W}^T \bm{X}^T \bm{X} \bm{W}\right)\right] \\ & = \underset{W}{\mathrm{argmax}}\left[\left( \sum\limits_{i=1}^d \omega_i^T \bm{X}^T \bm{X} \omega_i\right)\right] \end{aligned}$$

与最大投影方差类似，我们可以依次找到$\omega_1,\cdots,\omega_d$的方向，注意$\omega_1$不需要正交约束。

两种理解的可视化

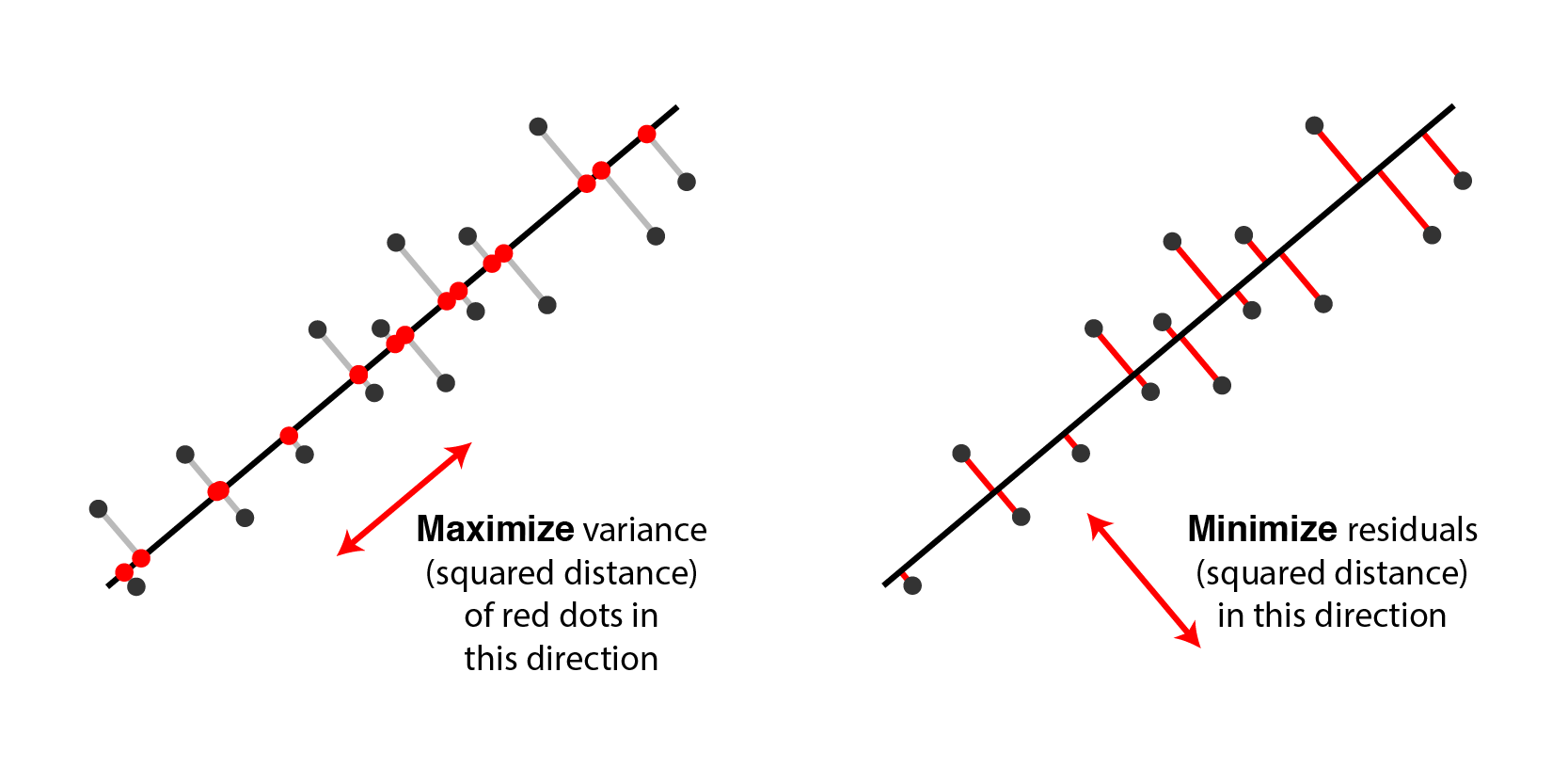
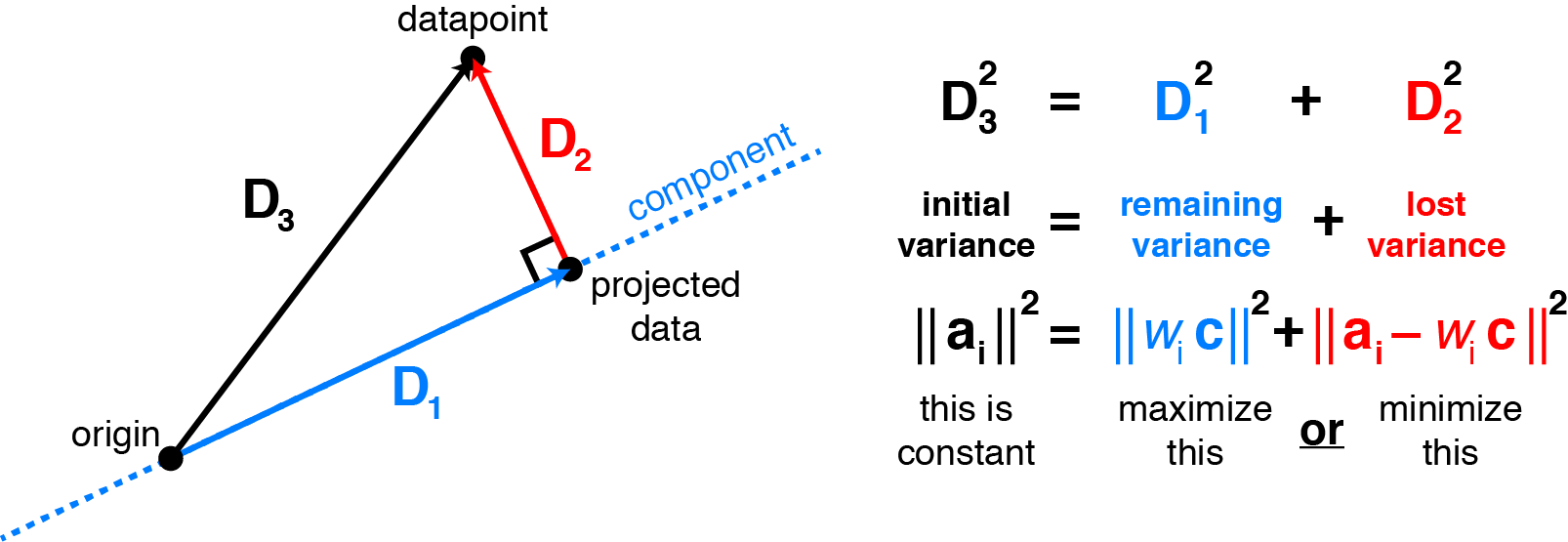
为何是全局最优？

那么下一个问题是如何证明这种逐个确定方向的贪心算法得到的解就是最优解？

可以通过数学归纳法来证明：首先，当$d=1$时，显然结论成立；然后，归纳假设为$d=k-1$时，以上方法得到的特征向量$(\omega_1, \cdots, \omega_{k-1})$是最优解；$d=k$时，假设存在一组基$(\omega’_1, \cdots, \omega’_k)$是最优解，注意到对$(\omega’_1, \cdots,\omega’_k)$做线性组合得到新的线性无关的基向量，重构误差不变。例如，对矩阵$\bm{W}$右乘一个单位正交矩阵$\bm{V}$（即$d$维空间的线性变换），投影矩阵变为

$$\bm{W}\bm{V}(\bm{W} \bm{V})^T = \bm{W}\bm{V}\bm{V}^T\bm{W}^T = \bm{W}\bm{W}^T$$

最后一个等号是因为$\bm{V}\bm{V}^T = \bm{I}$。我们希望找到一组基向量，其中$\omega_d’$与$(\omega_1,\cdots,\omega_{k-1})$正交（这一点总是可以做到的，因为$(\omega_1’, \cdots,\omega_k’) \in \mathcal{R}^k, (\omega_1’, \cdots,\omega_{k-1}) \in \mathcal{R}^{k-1}$）。在以上的优化算法中，$\omega_k$是第$k$大的特征值对应的特征向量，也是在满足约束条件$\omega_k$与$(\omega_1,\cdots,\omega_{k-1})$正交时的最优解，因此优化函数$F(\omega_k) \geq F（\omega_k’）$。同时，根据$k-1$时的归纳假设，$(\omega_1,\cdots,\omega_{k-1})$是$d=k-1$时的最优解，那么$(\omega_1,\cdots,\omega_k)$即为$d=k$时的最优解。

References

1. [机器学习]PCA（知乎）
2. Why does PCA maximize total variance of the projection?(StackExchange)
3. Everything you did and didn’t know about PCA